Devoirs de Vacances: La gamme de Pythagore

Joël archives 2008 …

Pourquoi la gamme que nous connaissons utilise-t-elle 7 degrés?

Pourquoi ces 7 degrés se succèdent-ils dans la séquence ton-ton-demi ton-ton-ton-ton-demiton ?

D'où vient cette succession des dièses (et des bémols) à la clé?

A la base du système se trouve une légende, la fameuse légende du forgeron de Pythagore.. Pythagore aurait découvert les quatre intervalles consonants (1: 2: 3: 4 = unisson, octave, quinte, quarte), ainsi que la seconde majeure non consonante (8 : 9), en entendant résonner l'enclume sous les coups de marteaux de poids différents....

Le principe de la gamme de Pythagore est basé sur une succession de quintes, la première harmonique entendue lorsque l'on joue une note.

	Si l'on part d'une fondamentale 1 que nous prenons comme unité de fréquence, la première quinte a pour fréquence 3/2 (en fait l’harmonique 3, qui, normalisée ((ramenée dans l'intervalle [1;2]), donne le rapport 3/2).
	Pythagore ayant noté qu'une note et sa quinte "sonnaient" bien ensemble, prit à nouveau la quinte de la note trouvée, sa fréquence est 3/2*3/2=9/4 qui, normalisée (ramenée dans l'intervalle [1;2]) donne 9/8.
	En prenant la quinte de la nouvelle note nous trouvons (3/2)³=27/8 qui, normalisée donne 27/16.
	La quinte suivante a pour fréquence (3/2)⁴=81/16 ce qui donne 81/64. A ce niveau, nous avons 5 notes assez régulièrement réparties et nous pourrions nous arrêter. Nous avons obtenu la gamme pentatonique majeure qui est utilisée en jazz sous sa forme tempérée, en particulier dans le "blues".
	La quinte suivante a pour fréquence (3/2)⁵= 243/32 ce qui donne 243/128.
	Nous avons maintenant 6 notes et, curieusement, la 7ème note n'est pas celle qui serait définie par la quinte suivante et qui se placerait pourtant dans l'intervalle un peu plus grand entre la 1^ère et la 4^ème quinte. Elle est calculée sur le fait que si 2 est en harmonie avec sa quinte, il est aussi en harmonie avec la note dont elle est la quinte et qui a pour fréquence 2/3 car 1=3/2*2/3 ce qui donne 4/3 dans l'intervalle [1;2].
	Nous avons maintenant les 7 notes de la gamme majeure de Pythagore.

Pour relier ces notes aux degrés que nous connaissons, il nous faut remonter au XI^e siècle, où le moine Guido d'Arezzo a l'idée d'utiliser des syllabes du chant grégorien l'Hymne de Saint Jean-Baptiste pour nommer les notes. Chaque vers de cet hymne commence par un son qui monte chaque fois d'un degré. Cette appellation s'est imposée face à la notation alphabétique toujours utilisée dans les pays germaniques ou anglo-saxons.

Hymne de Saint Jean-Baptiste

Ce chant, dont le texte latin a été écrit par le poète Paul Diacre, est composé des vers suivants (en gras, les syllabes utilisées pour nommer les notes) :

Ut queant laxis
Resonare fibris
Mira gestorum
Famuli tuorum
Solve polluti
Labii reatum
Sancte Iohannes

Par la suite , on contesta que la syllabe Ut était peu pratiquable pour le chant : on lui substitua donc le « Do » de Domine au XVIII^e siècle. Nous avons alors:

Mais revenons à la gamme de Pythagore

Calculons les rapports de fréquences entre notes successives :

Nous n'avons que des rapports de 9/8 (tons pythagoriciens) et des rapports de 256/243 (demi-tons pythagoriciens) que nous retrouvons dans l'ordre que nous connaissons dans notre gamme actuelle : 1 ton - 1 ton - 1 demi-ton - 1 ton - 1 ton - 1 ton - 1 demi-ton.

On remarque que le ton est un peu supérieur à la succession de deux demi-tons.

Justifions cette affirmation par un calcul, pas si simple que cela et qui montre la difficulté à travailler avec des notions où seuls les rapports entre les nombres importent.

Si nous allons d'une note A à une note B par un demi-ton puis de la note B vers la note C par un demi-ton nous avons :

qui est un rapport un peu plus grand.

Pour être plus précis, le rapport des fréquences est :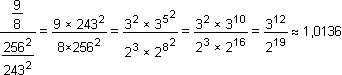
.

Cette différence de l'ordre de 1/9 de ton n'est pas négligeable et tout à fait audible, elle s'appelle le comma pythagoricien.

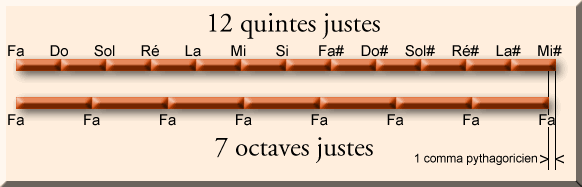
Ce comma Pythagoricien, nous le retrouvons en rapprochant la gamme de Pyhagore de la gamme tempérée que nous connaissons bien. Douze quintes justes valent à peu près 7 octaves justes, l’à peu près étant précisément le comma pythagoricien.

Si vous vouliez en savoir davantage, et découvrir la quinte du loup..., lire les beaux articles suivant:
. La Gamme Pythagoricienne
. La Gamme de Pythagore
. La gamme naturelle ou de Zarlino
. La Gamme tempérée

Devoirs de Vacances:

1) Transcire en neumes l'hymne de Saint Jean-Baptiste:

2) Le chanter et l'apprendre par coeur, le transposer en sol M

3) Distinguer parmi les enregistrements suivant les gammes de Pythagore et tempérée (Nécessite "Adobe FLASH Player") :

Gamme 1
Gamme 2

4) Exercer la finesse de votre oreille en discernant le Fa# du Sol b dans la succession suivante, mémoriser le comma pythagoricien qui les sépare:

Les copies sont à remettre avant la rentrée...

Bon été à toutes et à tous.

Musicalement votre,

Joël C.

Bibliographie:
Jean-Luc Juveneton : Ingénierie Educative - CRDP - Grenoble (38)
Traité d'Acoustique -Lord Rayleigh
Wikipedia

Retour à l'accueil